When I started with the STorM32 gimbal controller project 5 years ago, I had some experience with controllers from my GA250 gyro firmware and GA250 FP&Coax gyro-mixer projects, but had zero idea about the control of a 3-axis direct-drive electro-mechanical system. I could fill some gaps in knowledge (here, here, here), but the controller design remained largely phenomenological. Two years ago I stumbled across the topics robotics and manipulators, realizing that this is what a gimbal is. So, I read a book on it and learned its techniques, and put it on my list of plans to rework the STorM32 gimbal controller along the robotics lines … but, I never did. Only recently I came back to this topic again, and found time to work out some results using the robotics mathematical tools … and realized that they essentially agree with what I had already implemented.
1. Basics
1.1. Coordinate Frames, 1.2. Rotation Rate, 1.3. Fundamental Gimbal Laws
2. YRP Representation
3. Denavit Hartenberg
3.1. Basics, 3.2. Yaw-Roll-Pitch Gimbal, 3.3. Yaw-Roll-Pitch Gimbal with Tilted Roll
4. Dynamics
4.1. Basics, 4.2. Robotics, 4.3. Manipulator with Actuator, 4.4. Cartesian Space
5. Gimbal Models
5.1. Gimbal Model I, 5.2. Gimbal Model II, 5.3. Gimbal Model III
References
1. Basics
Summary of some fundamental relations relevant for gimbals of all kinds. ![]() are the parameters describing the orientation of the camera with respect to the fixed frame and
are the parameters describing the orientation of the camera with respect to the fixed frame and ![]() those describing the orientation of the gimbal base. The parameters
those describing the orientation of the gimbal base. The parameters ![]() describe the configuration of the gimbal, i.e., the orientation of the camera with respect to the gimbal base; they typically would be the motor angles.
describe the configuration of the gimbal, i.e., the orientation of the camera with respect to the gimbal base; they typically would be the motor angles.
1.1. Coordinate Frames
Earth fixed: ![]() , indexed with superscript
, indexed with superscript ![]()
Camera fixed: ![]() , indexed with superscript
, indexed with superscript ![]()
Gimbal base: ![]() , indexed with superscript
, indexed with superscript ![]()
Coordinate Transformations:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
1.2. Rotation Rate
![]()
![]()
![]() with
with ![]()
![]() with
with ![]()
more precisely:
![]()
![]()
![]() with
with ![]()
![]()
![]()
![]()
![]() rotation rate of frame
rotation rate of frame ![]() , expressed in frame
, expressed in frame ![]()
![]() rotation rate of frame
rotation rate of frame ![]() , expressed in frame
, expressed in frame ![]()
1.3. Fundamental Gimbal Laws
![]()
If the same representation is used for the three orientations, it holds: ![]()
![]()
Rotation rate in frame ![]() due to changes in angles
due to changes in angles ![]() :
:
![]()
Rotation rate in frame ![]() due to changes in angles
due to changes in angles ![]() :
:
![]()
Rotation rate in frame ![]() due to changes in angles
due to changes in angles ![]() :
:
![]()
Rotation rate in frame ![]() due to changes in angles
due to changes in angles ![]() :
:
![]()
Comment: Strapdown gyros in frame ![]() and
and ![]() measure
measure ![]() and
and ![]() , respectively.
, respectively.
2. YRP Representation
The yaw-roll-pitch (YRP) representation of the angles is well suited for gimbals in Pitch-Roll-Yaw configuration.
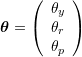
Rotation Matrix Yaw-Roll-Pitch:
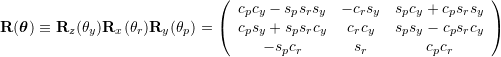
Jacobian Yaw-Roll-Pitch:
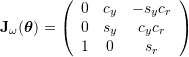 ,
, 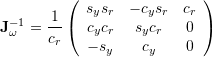
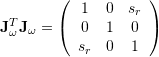
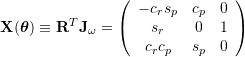
![]()
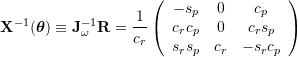
![]()
Usefull:
![]()
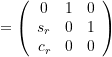
![]()
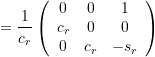
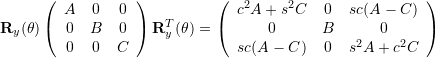
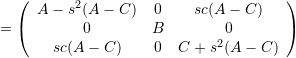
![]()
![]()
![]()
![]() (only revolute joints)
(only revolute joints)
![]()
![]() (only revolute joints)
(only revolute joints)
DH Conditions:
DH1: axis ![]() is perpendicular to axis
is perpendicular to axis ![]()
DH2: axis ![]() intersects axis
intersects axis ![]()
(): axis ![]() is along rotation or slide axis
is along rotation or slide axis
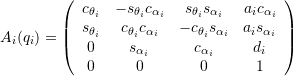
![]() : angle to rotate
: angle to rotate ![]() to
to ![]() around
around ![]() axis
axis
![]() : angle to rotate
: angle to rotate ![]() to
to ![]() around
around ![]() axis
axis
![]() : displacement along axis
: displacement along axis ![]()
![]() : displacement along axis
: displacement along axis ![]()
DH Matrices:
![]() ,
, ![]() ,
, ![]() ,
, ![]() :
: 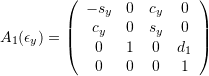
![]() ,
, ![]() ,
, ![]() ,
, ![]() :
: 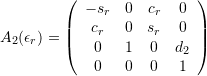
![]() ,
, ![]() ,
, ![]() ,
, ![]() :
: 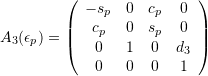
Comment: With respect to rotation, the matrices correspond to ![]() .
.
Comment: The offset ![]() can be set to zero without restriction of generality, and for a balanced gimbal
can be set to zero without restriction of generality, and for a balanced gimbal ![]() should be zero. Thus, only
should be zero. Thus, only ![]() should be of relevance.
should be of relevance.
Manipulator Matrices:
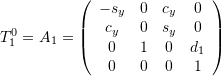
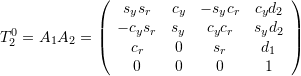
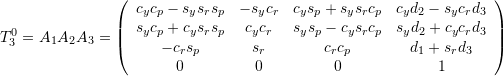
![]()
Manipulator Jacobian:
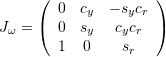
![]()
![Rendered by QuickLaTeX.com J_v = \left[ z^0_0 \times o^0_n, z^0_1 \times o^0_n, z^0_2 \times o^0_n \right] - \left(\begin{array}{ccc} 0 & s_y d_1 & c_y c_r d_1 - s_y s_r d_2 \\ 0 & -c_y d_1 & s_y c_r d_1 + c_y s_r d_2 \\ 0 & 0 & -c_r d_2 \end{array}\right)](https://www.olliw.eu/wp-content/ql-cache/quicklatex.com-0b25eb03b5fd2e9f63ca5c9086c46b25_l3.png)
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
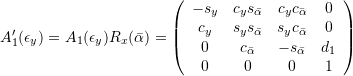 ,
, ![]() ,
, ![]()
4. Dynamics
4.1. Basics
![]()
![]()
![]()
4.2. Robotics
Lagrange:
![]()
Equation of Motion:
![]()
![]()
![]()
Note: The matrix ![]() is the transpose of
is the transpose of ![]() .
.
![]()
![]()
![]()
Gimbals are balanced, thus ![]() .
.
Kinetic Energy:
The energy in the Lagrange function is additive. Therefore each arm contributes additively to the Lagrange function as well as to the equation of motion.
![]()
![]()
Generalized Inertia Matrix:
![]()
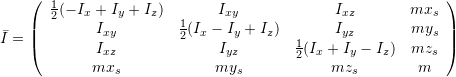
4.3. Manipulator with Actuator
Actuator:
![]()
![]()
![]()
![]()
Equation of Motion:
![]()
![]()
![]()
4.4. Cartesian Space
![]()
![]()
![]()
![]()
![]()
![]()
![]() (if
(if ![]() is invertible, otherwise use pseudoinverse)
is invertible, otherwise use pseudoinverse)
![]()
![]()
![]()
![]()
Comment: ![]() is symmetric and positive definite as
is symmetric and positive definite as ![]() is. For
is. For ![]() this doesn’t hold true.
this doesn’t hold true.
5. Gimbal Models
The following gimbal models assume a gimbal in pitch-roll-yaw configuration, i.e., the matrices given in the above chapters Denavit Hartenberg or YRP Representation do apply.
5.1. Gimbal Model I
It is assumed that all mass is concentrated in the camera, and that the camera’s moment of inertia matrix is proportional to unit.
![]()
![]()
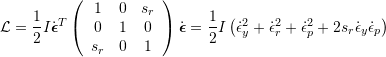
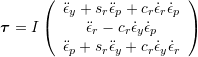
5.2. Gimbal Model II
It is assumed that all mass is concentrated in the camera, and that the camera’s moment of inertia matrix is diagonal.
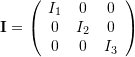
![Rendered by QuickLaTeX.com \mathcal{L} = K_{rot} = \dfrac{1}{2} \dot{\boldsymbol{\epsilon}}^T \left( {\bf{X}}^T {\bf{I}} {\bf{X}} \right) \dot{\boldsymbol{\epsilon}} = \dfrac{1}{2} \dot{\boldsymbol{\epsilon}}^T \left[ \left(\begin{array}{ccc} 0 & s_r & c_r \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right) {\bf{R}}_y(\epsilon_p) {\bf{I}} {\bf{R}}^T_y(\epsilon_p) \left(\begin{array}{ccc} 0 & 1 & 0 \\ s_r & 0 & 1 \\ c_r & 0 & 0 \end{array}\right) \right] \dot{\boldsymbol{\epsilon}}](https://www.olliw.eu/wp-content/ql-cache/quicklatex.com-f979c3278b66fe19d725c2ab09082b5c_l3.png)
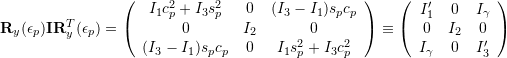
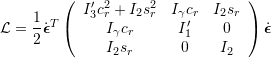
![]()
Comment: ![]() ,
, ![]() ,
, ![]() .
.
Comment: To minimize axis coupling one should attempt ![]() and
and ![]() . In this regard GoPro-style cameras are better than Mobius-style cameras.
. In this regard GoPro-style cameras are better than Mobius-style cameras.
Comment: ![]()
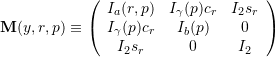
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.3. Gimbal Model III
It is assumed that the moment of inertia matrices of the camera and the roll and yaw arms are diagonal, and that the center of masses of the camera and roll arm coincide and fall onto the yaw rotation axis (![]() ). The Lagrangian consists then of only the rotational energies of the camera, roll and yaw arms.
). The Lagrangian consists then of only the rotational energies of the camera, roll and yaw arms.
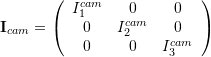
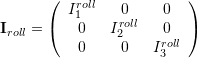
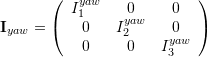
![]()
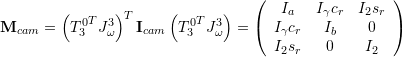
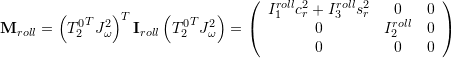
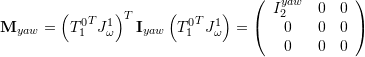
![]()
![]()
![]()
Comment: The result for ![]() had been calculated already in gimbal model II.
had been calculated already in gimbal model II.
Comment: It holds ![]() ,
, 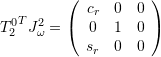 ,
, 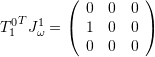
Comment: The moment of inertia matrices are with respect to the respective joint frames, and not the manipulator base frame.
With a more natural labeling of the moment of inertia values, the diagonals in the total ![]() matrix can be written as:
matrix can be written as:
![]()
![]()
![]()
Comment: Both ![]() and
and ![]() should be zero, see a comment in the above. Only
should be zero, see a comment in the above. Only ![]() is of relevance. which should however add a constant moment of inertia to the yaw axis dynamics, and thus can be absorbed into
is of relevance. which should however add a constant moment of inertia to the yaw axis dynamics, and thus can be absorbed into ![]() . The major assumption in the gimbal model III is thus that the moment of inertia matrices are diagonal, which often won’t be true for the roll arm, and is unrealistic for the yaw arm.
. The major assumption in the gimbal model III is thus that the moment of inertia matrices are diagonal, which often won’t be true for the roll arm, and is unrealistic for the yaw arm.
Appendix: References
[MS] Robot Dynamics and Control [.pdf] – by M.W. Spong, S. Hutchinson, and M. Vidyasaga.
[RJ] Theory of Applied Robotics[.pdf] – by R.N. Jazar.
[FL] Robot Manipulator Control: Theory and Practice [.pdf] – by F.L. Lewis, D.M. Dawson, and C.T. Abdallah
[RM] A Mathematical Introduction to Robotic Manipulation, A Mathematical Introduction to Robotic Manipulation [.pdf] – by R. M. Murray, Z. Li, and S. S. Sastry

