The Simplest Reasonable Camera Gimbal Model and Control Law

15. Okt. 2021 | Letzte Änderung 17. Okt. 2021 | Thema Brushless Gimbal, Grundlagen
Tag , ,

Considering that the STorM32 gimbal controller project is now many years old, this is something I really should have written up long ago. But I didn’t. I recently came back to the topic while working on some stuff and constantly required it as a reference. So, here it is. 🙂

This article will start with presenting a model which may look perfectly reasonable, and which indeed provides valuable insight. However, it is fundamentally flawed and hence does not qualify as „simplest and reasonable“ model. The improved model is the main topic of the article, and will be presented in the subsequent chapters.

It is important to properly state what the goal of using a gimbal is. Obviously, the goal is to stabilize the orientation (attitude) of a camera, and to do so in the presence of disturbances. All clear, right. There are however different sources of disturbances, and we have to distinguish them properly. One type of disturbance are forces/torques acting on the camera or gimbal structure in general, such as wind, and so on. Another type is a motion of the gimbal base. In fact, that’s what we do mostly with a gimbal, namely to move around the gimbal base and yet having a steady camera. So, the immediate conclusion is:

The primary goal of a gimbal is disturbance rejection, and the rejection of movements of the gimbal base in particular.

Sure, we also may want to change the camera’s orientation through some controls such as joysticks or serial commands. But this is not the primary reason why we use a gimbal; we use it to have a stabilized camera in the wake of gimbal-base movements. As simple as it is, this is a most crucial insight when we want to talk about gimbal performance. I want to add that depending on the application also the torque disturbances can be very relevant, such as in planes.

We will consider only a 1-axis gimbal, because only then the model is really simple. For 2- and more so 3-axis gimbals the dynamical equations are so complicated even in simple approximations that any analytical treatment becomes cumbersome (see link). Even worse, as I just stressed, we need to also include the dynamics of the gimbal base if we want to understand disturbance rejection, which would add 3 more „axes“ and we would face a 6-axis robot system! The general problem is then really just intractable analytically (at least for mortals like me). I could not find any literature on gimbals which would consider the „moving base“ situation or provide approximations one could deal with, and I myself for sure was also not able to come up with approximate model equations. Hence, 1-axis gimbal only. All we can do is to hope that some conclusions may somehow be applicable to a 3-axis gimbal.

1. Basics
2. Simplest, but flawed, Gimbal Model
  2.1. Dynamics, 2.2. Control Law, 2.3. Why the model is flawed
3. Simplest Reasonable Gimbal Model
  3.1. Dynamics, 3.2. Check if the model makes sense
4. Controller
  4.1. Control Law, 4.2. P Controller, 4.3. D Controller, 4.4. PD Controller, 4.5. Effect of an I Term, 4.6. Torque Disturbances
5. Concluding Words


1. Basics

Before we start, let’s write down some general results.

Thanks to the simple geometry of the gimbal, we easily come up with this geometrical relationship which describes the gimbal:

  \theta_1 = \theta_2 + \epsilon

\theta_1 : tilt of the gimbal camera arm and camera
\theta_2 : tilt of the gimbal base
\epsilon : angle of the motor at the joint

We also will need a model for the motor. Here we have to differentiate how the motor is driven, we consider full FOC, simple FOC, and sinusoidal drive, which are described by these motor models:

FOC:   \tau_M = K u - B \dot{\epsilon}
sin:    \tau_M = K u - K \epsilon - B \dot{\epsilon}

u : motor control input
K : motor constant
B : motor friction

The equations were written here such as to make the look as equally as possible; the K and B constants can be quite different for the different drives however. For the details please see Field Oriented Control: To FOC or not to FOC. For instance, for full FOC we would have K = \frac{k p \Psi_p}{R}, u = i_0, and B = 0.

It is interesting to note that for the simplified FOC and sinusoidal drives B \ne 0, i.e., these drive schemes produce a „flux friction“, which appears in addition to any mechanical friction.

The additional K \epsilon term for the sinusoidal drive makes this drive very different, and is the origin of all the difficulties with it. You can find a couple of articles discussing this on my pages.


2. Simplest, but flawed, Gimbal Model

2.1. Dynamics

Besides the gimbal equation and the motor model we need a model for the gimbal dynamics, which should include the motor torque, mechanical friction in the joint, and so. The obvious model is

  I \ddot{\epsilon}} = -b_f \dot{\epsilon} + \tau_M + \tau_d

I : inertia of the camera gimbal arm including the camera
b_f : viscous friction coefficient
\tau_M : torque produced by the motor
\tau_d : torque disturbance acting on the camera

We can combine this with the motor equation to define the process transfer function:

FOC:   G_P(s) = \dfrac{K}{b s + I s^2}
sin:    G_P(s) = \dfrac{K}{K + b s + I s^2}

where b = b_f + B.

Please note the fundamental difference between these two transfer functions.

 
1.2. Control Law

All we need to do now is to write down our control law, and close the feedback loop:

  u = G_C(s) (\theta_0 - \theta_1)

  \theta_1 = \dfrac{G_C G_P}{1 + G_C G_P} \theta_0 + \dfrac{1}{1 + G_C G_P} \theta_2 + \dfrac{G_P}{1 + G_C G_P} \dfrac{1}{K} \tau_d

\theta_0 : control input, setpoint

This is a pretty ordinary control law. However, it also clearly shows us what makes discussing a gimbal different to essentially all other systems we typically deal with, such as flight controllers, servo controllers, and so on. In the latter cases the primary objective is the response with respect to the control input \theta_0, i.e., the tracking behavior. In the case of a gimbal the primary objective is the response with respect to the gimbal base \theta_2, i.e., the output disturbance rejection! Given that the widely known tuning rules are targeted at optimizing the tracking, we also realize that these won’t directly apply here. Lastly, we learn that torque disturbances enter as input disturbances.

So, this simple model has given us two important insights:

• Tuning a gimbal means tuning the controller for best (output) disturbance rejection, not tracking.

• The widely known tuning rules do not obviously apply to the case of a gimbal.

 
2.3. Why the model is flawed

You may now be surprised to hear that the above model is fundamentally flawed. I will demonstrate this by a simple Gedanken experiment. We will learn that the above model is in fact only valid if \theta_2 is constant, i.e., when the gimbal base is not moving (or very slowly moving). But wasn’t this exactly what we wanted to study, a moving gimbal base?

In order to see the flaw, let’s consider a gimbal which is connected at the joint only through a bearing, i.e., there is no motor and no motor torque. Clearly, if the friction in the bearing is exactly zero, then the camera should not move at all when we move (tilt) the gimbal base. This is so because the camera has inertia, I \ne 0. In this situation, since there are no torques acting on the camera, the equation of motion for the camera would be

  I \ddot{\theta_1} = 0   if   b_f = 0

Now let’s assume that there is some friction in the bearing. Clearly, now we expect that we can tilt the camera by tilting the gimbal base. However, we also expect that this depends on how fast we tilt the gimbal base. If we would tilt the gimbal base very fast, we expect that the camera should not move (or not move much), that is

  \dot{\theta_1} \approx 0   if   \dot{\theta_2} \rightarrow \infty

In contrast, if we would tilt the gimbal base very slowly then the camera should nicely follow, that is

  \theta_1 \approx \theta_2   if   \dot{\theta_2} \rightarrow 0

Let’s see if the above model can describe that. We set b_f = \tau_M = \tau_d = 0 and arrive at

  I \ddot{\epsilon}} = 0

However we also have \theta_1 = \theta_2 + \epsilon and thus

  \ddot{\theta_1} = \ddot{\theta_2}   !!!!!

That is, the model predicts that the camera is following the gimbal base when it is tilted! According to our Gedanken experiment this corresponds to the case when the gimbal base is tilting only very slowly. This will be shown strictly below. We may also get an idea of what the problem is, namely that there is I \ddot{\epsilon}} and not I \ddot{\theta_1} on the left-hand-side of the equations. We can double-check by also allowing friction:

  I \ddot{\epsilon}} = -b \dot{\epsilon}}

which implies \dot{\theta_1} = \dot{\theta_2} and which is equally faulty.


3. Simplest Reasonable Gimbal Model

3.1. Dynamics

There are various ways to derive the correct dynamic equations. For instance, we could open a robotics text book and look up the results for a „two-link planar elbow manipulator“, and adapt them to our case. This may give us a certain level of satisfaction and confidence in the result, but let’s try to derive it more straight forwardly (it will of course agree with that obtained from using the robotics theory machinery).

Let’s first note that we are not interested in the dynamics of the gimbal base (or gimbal arm connecting gimbal base and motor), but only in the dynamics of the camera. That is, the appropriate starting point is Newton’s equation for the camera:

  I \ddot{\theta_1} = \tau

where \tau are all torques acting on the gimbal. Friction in the joint is clearly related to the relative motion of the two gimbal arms, and thus adds a term -b_f \dot{\epsilon}. Note that this produces a coupling between camera and gimbal base. Disturbance torques which act on the camera are obviously incorporated by adding a term \tau_d. Accounting for the effect of the motor might be more confusing, as it exerts torques on both gimbal arms. However, we can apply Newton’s „actio = reactio“ here to find that the motor torque acts on the camera with \tau_M and on the gimbal base with -\tau_M (Newton’s 3rd law applies since there are no other forces/torques in our scenario). Thus, there will be a torque on the gimbal base due to the motor, but this is not what we are interested in. So, all we need to do is to add a term \tau_M to the torque acting on the camera. Thus:

  I \ddot{\theta_1} = -b_f \dot{\epsilon} + \tau_M + \tau_d

3.2. Check if the model makes sense

Let’s check if this result can describe our above Gedanken experiment. First, we again assume zero friction in the joint, i.e., set -b_f = \tau_M = \tau_d = 0. We obtain

  I \ddot{\theta_1} = 0   if   b_f = 0

This is exactly what we were expecting. The camera does not tilt irrespective of the tilting of the gimbal base. Perfect. Let’s also check the case with friction in the joint. Now we obtain

  I \ddot{\theta_1} = -b_f \dot{\epsilon}

which we rewrite as

  I \ddot{\theta_1} + b_f \dot{\theta_1} = b_f \dot{\theta_2}   or   \theta_1(s) = \dfrac{b_f}{b_f + I s} \theta_2(s)

This makes perfect sense. When we tilt the gimbal base slowly, which corresponds to s \rightarrow 0, we obtain \theta_1 = \theta_2, i.e., the camera follows the gimbal base, as we expect it. When we tilt the gimbal base very fast, which corresponds to s \rightarrow \infty, we obtain \theta_1 = 0, i.e., the camera does not tilt but stays steady due to its inertia, also as expected. Perfect.

Moreover, we see that the behavior corresponds to that of a low-pass filter of 1st order, with a characteristic frequency \omega_c = \frac{b_f}{I}. Also this makes perfect sense: For a larger friction we expect that the gimbal base needs to be moved more abruptly in order keep the camera steady or that the camera will follow better at slow gimbal base movements. Vice versa, for a larger inertia of the camera we expect the opposite trend. In other words, it is the ratio \frac{b_f}{I} which matters, and it should be as small as possible for this simple mechanical (non-motorized) gimbal. Which makes perfect sense.


4. Controller

4.1. Control Law

Again, all we need to do is to use the control law and close the feedback loop:

  \theta_1 = \dfrac{G_C G_P}{1 + G_C G_P} \theta_0 + \dfrac{1}{1 + G_C G_P} \dfrac{b}{b +I s} \theta_2 + \dfrac{G_P}{1 + G_C G_P} \dfrac{1}{K} \tau_d

Let us write it more compactly as

  \theta_1 = G_{\theta_0}(s) \theta_0 + G_{\theta_2}(s) \theta_2 + G_{\tau_d}(s) \tau_d

G_{\theta_0}(s) : tracking response
G_{\theta_2}(s) : gimbal-base motion rejection
G_{\tau_d}(s) : torque disturbance rejection

The process transfer functions G_P(s) for the various drives are defined as before.

This is interesting: The tracking behavior as well as the input disturbance rejection of \tau_d is the same as for the simple flawed model. However, the output disturbance, i.e., response to \theta_2, is now additionally low-pass filtered.

Also noteworthy, the friction term b enters now, and not only b_f as for the motor-less gimbal. That is, FOC control has some advantage here over the simplified FOC and sinusoidal drives (recall, the friction should be as small as possible, and full FOC does not add „flux“ friction).

 
4.2. P Controller

Let us understand the behavior with a P controller:

  G_C(s) = K_P

For the gimbal-base motion rejection, assuming a FOC scheme, we obtain

  G_{\theta_2}(s) = \dfrac{b s}{K_P K + b s + I s^2}

This can be nicely rewritten by using the characteristic frequency \omega_c = b / I, which we found before, and the resonance frequency \omega_0^2 = K_P K / I, and normalizing frequencies to \omega_c:

  S \equiv \dfrac{s}{\omega_c} = \dfrac{b}{I} s

  \Omega_0^2 \equiv \dfrac{\omega_0^2}{\omega_c^2} = \dfrac{K_P K I}{b^2}

  G_{\theta_2}(S) = \dfrac{S}{\Omega_0^2 + S + S^2}

For K_P = 0 or open-loop we get the behavior of a motor-less gimbal with just a joint and friction, i.e., the situation which we considered in the above. It is described by a 1st-order low-pass behavior with a characteristic frequency \omega_c, i.e., gimbal-base motions are rejected only at frequencies above \omega_c.

For K_P > 0, the transfer function corresponds to that of a 2nd-order band pass, with the properties

resonance frequency:   \omega_0^2 = \dfrac{K_P K}{I}
resonance amplitude:   A_0 = 1
bandwidth:          BW = \omega_c = \dfrac{b}{I}
quality factor:        Q = \Omega_0 = \dfrac{\omega_0}{\omega_c} = \sqrt{ \dfrac{K_P K I}{b^2} }

That is, thanks to the motor and controller, gimbal-base motions are now indeed rejected at low frequencies, which is exactly what we want. We can push this range up by increasing the control gain K_P. However, we cannot push it up too high, of course, since the control loop would become unstable. Also note that the maximum amplitude of the transfer function is always one. There is thus always a frequency range, around the resonance frequency, where there is no disturbance rejection at all, which is certainly undesired. One further can note that the band width is constant and that the quality factor thus increases with K_P, i.e., the transfer function becomes sharper and sharper.

At high frequencies, above the resonance frequency, the roll-off is \propto 1/s, similar as for the non-motorized gimbal. That is, at these frequencies the motor and controller are not helping in any way and gimbal-base motion rejection is provided only by the ratio of friction vs camera inertia, b/I.

 
4.3. D Controller

We now choose a D controller:

  G_C(s) = K_D s

You may find this surprising, since D controllers are not usually used, and indeed, the fact that we consider it should not be taken as indication that it is suggested to be used.

The gimbal-base motion rejection, again assuming a FOC scheme, now becomes

  G_{\theta_2}(s) = \dfrac{b}{(b + K_D K) + I s}

This is a 1st-order low pass, like for the gimbal with no motor. However, the amplitude is reduced by a factor (1 + \frac{K_D K}{b}), which means improved gimbal-base motion rejection. Unfortunately, this comes at a cost, namely the characteristic frequency is increased to \omega_c' = (b + K_D K) / I. That is, the D controller actually worsens the gimbal-base motion rejection at higher frequencies.

At this point, lets emphasize again that we consider here the response concerning gimbal-base motions or \theta_2. The controller stability is however given by the response with respect to the setpoint \theta_0 or tracking response function G_{\theta_0}(s), respectively. We should not forget that we always have to also investigate this response function, before we get too excited about what we can achieve.

 
4.4. PD Controller

Now we choose a PD controller:

  G_C(s) = K_P + K_D s

For the gimbal-base motion rejection, again assuming a FOC scheme, we obtain

  G_{\theta_2}(s) = \dfrac{b s}{K_P K + (b + K_D K) s + I s^2}

This is also a 2nd-order band-pass as for the P controller. That is, adding the D-term has not fundamentally changed the transfer function as compared to that of a pure P controller. The bandwidth is somewhat affected, but the resonance frequency in fact not. The most important effect is that the resonance amplitude is reduced:

resonance amplitude: 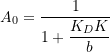  A_0 = \dfrac{1}{1 + \dfrac{K_D K}{b} }

That is, the main effect of the D-term is to suppresses the resonance amplitude, which allows us to improve the gimbal-base motion rejection at all frequencies. This is similar to what we have found for the D controller. Fortunately, in contrast to the D controller, the behavior at higher frequencies is however not negatively affected, but rather improved. Indeed, the resonance frequency is not affected, \omega_0^2 = \dfrac{K_P K}{I}, and still is determined by K_P only. Furthermore, the band width increases to BW = \omega_c' = \dfrac{b + K_D K}{I}, i.e., the quality factor becomes smaller and the transfer function less sharp. This also helps us when pushing the tuning towards higher frequencies.

 
4.5. Effect of an I Term in the Controller

As always, we can now also add an I-term to the controller, i.e., a term of the form K_I \frac{1}{s}. For as long as the I-term does not become too large, its effect is easy to understand: It simply adds an additional roll-off of \frac{1}{s} at low frequencies, which further improves the behavior at low frequencies. We certainly want to benefit from that, and thus would always opt to add an I-term to the controller.

However, in the case of the FOC drives, it does not really affect the controller stability (if K_I is not too high of course), and adding an I-term would not allow us to achieve e.g. significantly higher K_P values. That is, in order to obtain good disturbance rejection at medium to high frequencies the key controller terms are K_P and K_D.

 
4.6. Torque Disturbances

So far we have looked at the gimbal-base motion rejection or transfer function G_{\theta_2}(s), for reasons discussed in the introduction. However, let us also briefly inspect the torque disturbance rejection. Torque disturbance rejection can in fact be equally or maybe even more important in certain applications, such as e.g. on planes. Planes usually do not shake as much as copters do, while wind disturbances are massively stronger due to the overall higher flying speeds.

Let us first discuss a gimbal without motor. The transfer function with respect to torque disturbances \tau_d is

  \theta_1(s) = \dfrac{1}{ b s + I s^2} \tau_d

That is, the effect of a torque acting on the camera becomes infinitely large at low frequencies. This makes perfectly sense. Let’s assume again the situation of zero friction. Then one obviously can move the camera „freely“ as there is no counter action of any sort which would prevent camera motion (the camera inertia only determines how „quickly“ the camera would react, but would not prevent the motion). Hence, this gimbal does not provide effective torque disturbance rejection.

For a P controller and a FOC motor drive we obtain

  G_{\tau_d}(s) = \dfrac{1}{K_P K + b s + I s^2}

This again can be tidied-up using the same conventions as before, which yields

  G_{\tau_d}(S) = \dfrac{1}{K_P K} \dfrac{\Omega_0^2}{\Omega_0^2 + S + S^2}

The transfer function corresponds to that of a 2nd-order low pass. At high frequencies, above the resonance frequency, there is a roll-off \propto 1/s^2 similar to the non-motorized gimbal. That is, here torque disturbance rejection is only provided by the inertia of the camera. At low frequencies, the response is flat with amplitude 1/(K_P K), and torque disturbance rejection is achieved. The rejection is the better the larger the controller gain K_P is.

Interestingly, or sadly, torque disturbance rejection is not improved by a D-term. It would be however by an I-term.


5. Concluding Words

From the discussion it is clear: The most important factor to achieve a good disturbance rejection is a high controller gain.

This is, in fact, a well-known rule of thumb which is generally observed for disturbance rejection. 🙂

Concerning controller stability, which as said before determines or limits the range of values for K_P and K_D, one finds that for the FOC drive schemes a PD controller is in fact fully appropriate and allows achieving high K_P (for FOC drives the P- and D-terms in the controller are most important, the I-term is of much less relevance).

It is recalled that the full FOC scheme has an advantage over the simplified FOC scheme, since it doesn’t add „flux“ friction, that is the value of b is smaller. This is may not be of so much relevance for the controller tuning, but as we have seen here b/I is the key characteristic determining gimbal-base motion rejection. A lower b is thus always an advantage, which cannot be compensated for by whatever controller.

The sinusoidal motor drive was not discussed here. The very different motor transfer function, which is that of a 2nd-order low pass, i.e., characterized by a constant frequency response below the resonance frequency and not a \propto 1/s behavior as for the FOC drives, makes the sinusoidal motor drive more complicated to discuss, and also much less favorable. The interested reader should have no difficulty to work it out following the above procedures. For the sinusoidal drive one needs to resort to additional „tricks“ in order to achieve comparable rejection performance, especially feed-forward of the gimbal-base motion (known in STorM32 parlance as „2nd IMU“).

Hinterlasse einen Kommentar