Auswuchten von Rotorblättern: Was die Schulphysik dazu sagt

Zum richtigen Auswuchten der Helikopter-Rotorblätter wurde schon unsagbar viel geschrieben, aber trotzdem taucht diese Diskussion in den Foren immer wieder auf, mit den immer selben Fragen und den immer selben halben Antworten. Im Folgenden möchte ich das Thema „endgültig“ abklären – zumindest soweit wie dies mit der Mechanik starrer Körper möglich ist.

Wen die Details nicht interessieren sondern nur die Schlussfolgerungen bzw. Auswuchtprozedur – einfach zum letzten Kapitel vorspringen :).

Beim Rotor sind, logisch, neben der Mechanik weitere Effekte zu berücksichtigen, wie die aerodynamischen Kräfte und Momente oder die Elastizität der Rotorblätter (und Rotorwelle), und streng genommen sind Rotorblätter dann ausgewuchtet wenn die Masseverteilung (Masse und Schwerpunktlage), Biege- und Torsionssteifigkeitsverteilung, und Form (aerodynamischen Kräfte) für alle Blätter genau gleich sind. Klar, das ist ein Ding der Unmöglichkeit. Bei manntragenden Helis wird hier wesentlich mehr Mühe reingesteckt, um z.B. auch die aeroelastischen Effekte anzugleichen. Bei uns Hobby-Modellpiloten beschränkt sich das Wuchten auf Methoden, bei denen der Rotor (beide Rotorblätter zusammen) weder schnell bewegt noch gebogen wird, also einen starren Körper darstellt.

Betrachtet man die vielen verschiedenen, teils sehr kreativen Anleitungen zum Auswuchten der Rotorblätter dann reduzieren sich diese letztlich (fast immer) auf die gleichen zwei Schritten, nämlich (i) Auswiegen der Massen (bzw. Gewichte) und (ii) Abgleichen der Blattschwerpunkte, welche auch oft als statisches und dynamisches Wuchten bezeichnet werden. Als ein gerne zitiertes Beispiel sei [1] genannt, oder [2].

An dieser Stelle sei gleich geklärt: Der Sprachgebrauch „statisches“ und „dynamisches“ Wuchten ist schlicht falsch. Alle mir bekannten im Web verfügbaren Literaturstellen (außer natürlich RC-Heliseiten) sind da absolut eindeutig:

 Statisches Auswuchten => Schwerpunkt liegt auf der Drehachse
 Dynamisches Auswuchten => Drehachse stimmt mit einer Hauptträgheitsachse überein

Dieser Link [3] und dieses (hervorragende!) Manuskript [4] mögen als Beweise reichen. Bei keiner der (mir bekannten) Wuchtmethoden im RC-Helibereich geht es darum die Drehachse mit einer Hauptträgheitsachse in Übereinstimmung zu bringen, d.h., alle unsere Methoden sind „statisch“. Darüber hinaus ist immer wieder das Argument zu hören, dass die Lage der Blattschwerpunkte egal sei und es daher unnötig ist diese anzugleichen. Begründet wird dies mit der Tatsache das Helis mit Einblattrotoren ja schliesslich auch fliegen (eines der vielen Beispiele hier), oder wird gar mit einer Rechnung „bewiesen“ (eines der vielen Beispiele hier). Die Argumente sind nicht falsch, aber es wird übersehen das nur weil etwas funktioniert es nicht auch gut oder gar ideal funktionieren muss. Wir werden unten darauf zurückkommen.

Neben den Methoden zum Auswuchten der Rotorblätter gibt es natürlich noch die Vorschläge zum Wuchten des gesamten Rotorkopfs. Das (hervorragende) Video [5] wird sehr häufig zitiert. Aber auch dafür sollten die Rotorblätter erst einmal vorab gewuchtet werden.

1. Rotorblatt Kenngrößen
2. Fliehkräfte
3. Blatthalter
4. Konuswinkel
5. Pendel und Blattwaagen
6. Ausbalancieren
7. Zusammenfassung und Schlussfolgerungen
Appendix: Literatur, Formelsammlung

1. Rotorblatt Kenngrößen

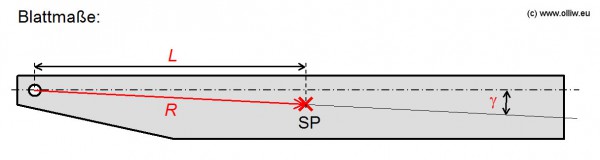
Für das Folgende sind einige Kenngrößen eines Rotorblatts relevant, die anhand des nachstehenden Bildes eingeführt werden sollen.

 : Masse
 : Schwerpunktslage
  oder : „echter“ Abstand des Blattschwerpunkts von der Blattwurzel
 : Vorlaufwinkel

2. Fliehkräfte

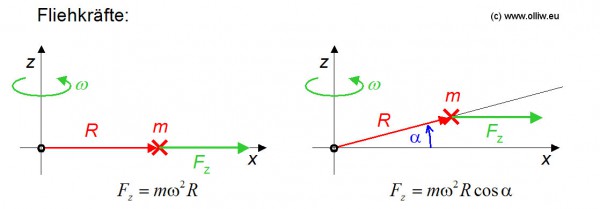
Zunächst betrachten wir einen Körper mit der Masse welcher sich im Abstand um eine Drehachse dreht. Jeder weis, es wirkt nun eine Fliehkraft welche den Körper nach aussen zieht. Dies ist im nachfolgenden Bild links dargestellt.

Den im Bild rechts gezeigten Fall wollen wir uns auch gleich überlegen, er wird später benötigen werden. Befindet sich der Schwerpunk des Köpers nicht wie im linken Bild senkrecht vom Befestigungspunkt, sondern steht unter einem Winkel , dann wirkt natürlich auch eine Fliehkraft. Diese geht allerdings senkrecht von der Drehachse weg, und die Stärke der Fliehkraft ergibt sich daher zu .

Nun betrachten wir zwei sich schnell drehende Rotorblätter. Für den Moment sollen diese nicht an einem echten Rotorkopf befestigt sein, sondern wir stellen uns beide direkt an der Blattwurzel mit der Rotorwelle verbunden vor (auf den Einfluss der Rotorblatthalter kommen wir noch). Ausserdem sollen nur die Fliehkräfte wirken; die aeroelastischen Effekte lassen wir aussen vor (auch dazu kommen wir später noch). Das ist genau die Situation wie sie so gerne z.B. in Foren diskutiert wird.

Es ist klar, die beiden Rotorblätter werden sich so ausrichten, dass die beiden Fliehkräfte genau entgegengesetzt wirken. Und es ist auch klar, das eine Unwucht verschwindet sobald die beiden Fliehkräfte genau gleich groß sind. Anders gesagt, es muss Kräftefreiheit herrschen, also

  .   Gl. (2.1)

Setzt man nun das obige Ergebnis für die jeweiligen Fliehkräfte ein dann erhält man sofort die

Einfache Fliehkraft-Bedingung:       Gl. (2.2)

Die Lage des Blattschwerpunkts ist in diesem einfachen Szenario tatsächlich egal. Es kommt nur drauf an, dass das Produkt aus Masse und Schwerpunktsabstand für beide Seiten des Rotors gleich groß sind. Deswegen können Helis mit Einblattrotoren fliegen, wie oben bereits festgestellt wurde.

Es ist allerdings zu bemerken, dass in Gl. (2.2) nicht die Blattschwerpunkstlage (siehe Kapitel 1) eingeht, sondern der tatsächliche Abstand von der Blattwurzel . Dieser wird mit vielen Auswuchtmethoden nicht bestimmt. Genauso geht auch die Vorspur der Blätter nicht in Gl. (2.2) ein. Wenn die Blätter unterschiedliche Vorspuren und haben, dann werden die Blattkanten nicht fluchten und die aerodynamischen Kräfte nicht ausgeglichen sein, und zu einem unrunden Lauf führen.

3. Blatthalter

Die Blätter werden ja nun nicht direkt an der Rotorwelle befestigt sondern an den (starren) Blatthaltern, was zu einem zusätzlichen Abstand führt und die Fliehkräfte verändert. Wie zuvor richten sich die Rotorblätter wieder genau so aus, dass die Schwerpunkte exakt gegenüber liegen, jetzt halt nur mit einen um vergrößerten Abstand von der Rotorwelle. D.h., die Fliehkraft-Bedingung ändert sich zu

  .     Gl. (3.1)

Es ist also nicht die einfache Fliehkraft-Bedingung Gl. (2.2) zu erfüllen, sondern Gl. (3.1). Blattwaagen, bei denen die Rotorblätter an einer Wippe aufgehängt werden (also so ein Teil wie z.B. hier), haben hier also gegenüber Auswuchthilfen (also so Teilen wie z.B. hier) einen gewissen Vorteil dahingehend, dass die Blatthalter-Länge zumindest in etwa mit berücksichtigt wird.

Die Gl. (3.1) können wir aber auch noch anders erfüllen, nämlich dadurch das wir der einfachen Fliehkraft-Bedingung Gl. (2.2) noch eine zweite Bedingung hinzugesellen. Einsetzen der Gl. (2.2) in Gl. (3.1) liefert die Zusatzbedingung oder

  .     Gl. (3.2)

Wenn aber und erfüllt sind, dann gilt offensichtlich auch ! Damit finden wir die

Erweiterte Fliehkraft-Bedingung:
  (1) ,     Gl. (3.3a)
  (2) oder .     Gl. (3.3b)

Erinnert das jetzt nicht bereits ein bischen an die zwei Schritte (i) Auswiegen der Massen und (ii) Abgleichen der Blattschwerpunkte?

4. Konuswinkel

Bisher hatten wir die aeroelastischen Kräfte nicht mit einbezogen, aber normalerweise wollen wir ja nicht nur mit Null-Pitch am Boden „schweben“. Eine volle Betrachtung dieser Effekte ist sehr kompliziert, und geht auch weit über meine Kompetenzen hinaus, aber wir können wenigsten den einfachsten Effekt mit berücksichtigen, nämlich den Schub der Rotorblätter.

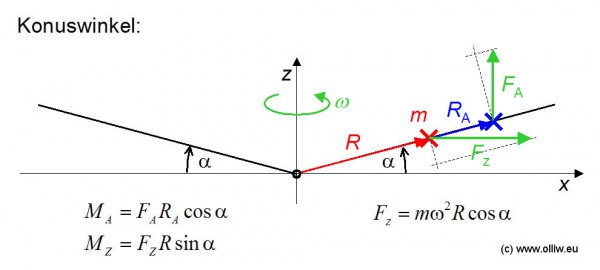
Der gesamte erzeugte Schub ergibt sich als die Summe der Beiträge der einzelnen Blattelemente und hängt in komplizierter Weise vom Anstellwinkel, den Verbiegungen, usw. ab. Wir können ihn uns aber als eine Kraft vorstellen, welche an einem Punkt (Druckpunkt) am Blatt angreift, wobei wir aber eben die Größe der Kraft sowie die Lage des Druckpunktes mit unseren Kenntnissen nicht bestimmen können. Ist auch nicht nötig. Im Allgemeinen wird der Druckpunkt und der Blattschwerpunkt nicht identisch sein. Bei einem steifen Rotorblatt sieht die Situation dann so aus wie im nachfolgenden Bild.

Da die Fliehkraft und die Schubkraft nicht am selben Punkt angreifen, können wir den Konuswinkel nicht über ein Kräfteparallelogram bestimmen, sondern müssen die jeweiligen Drehmomente betrachten. Der Konuswinkel ergibt sich dann aus dem Drehmomentgleichgewicht

  ,     Gl. (4.1)

oder auf die Beträge bezogen, (das obige Bild ist also unrealistisch; die Schubkraft ist viel zu groß gezeichnet). Die Drehmomente sind im obigen Bild berechnet, und Einsetzen ergibt

  .     Gl. (4.2)

Nun betrachten wir wieder zwei Rotorblätter, die allerdings aeroelastisch perfekt identisch sein sollen (für mehr reichen unsere Kenntnisse eben nicht). Der Wert soll also für beide Blätter übereinstimmen. Zudem soll der Spurlauf passen, d.h., dass der Winkel für beide Blätter gleich ist. Damit ergibt sich aus Gl. (4.2) die

Konuswinkel-Bedingung:       Gl. (4.3)

Man beachte den kleinen aber feinen Unterschied zur einfachen Fliehkraft-Bedingung: Die Schwerpunktsabstände gehen hier zum Quadrat ein!

Die Betrachtung der radialen Kräfte (senkrecht zur Drehachse) führt wieder zur einfachen Fliehkraft-Bedingung Gl. (2.2), da hat sich also nichts geändert. Wollen wir aber auch einen perfekten Spurlauf erreichen, so ist zusätzlich noch die Konuswinkel-Bedingung zu erfüllen. Wie lassen sich nun beide Gleichungen gleichzeitig erfüllen? Einfach, wenn Gl. (2.2) gilt, dann ergibt sich aus Gl. (4.3) die Forderung ! Nun können wir aus Kapitel 3 abschreiben: Wenn und erfüllt sind, dann gilt offensichtlich auch ! Damit finden wir wieder die erweiterte Fliehkraft-Bedingung Gl. (3.3). Erinnert uns das jetzt nicht schon wieder an die zwei Schritte (i) Auswiegen der Massen und (ii) Abgleichen der Blattschwerpunkte?

In der Überlegung wurde angenommen, dass die Rotorblätter freibeweglich am Rotorkopf befestigt sind (Schlaggelenke), was bei unseren Modellhelis nicht bzw. selten der Fall ist. Zusätzlich werden oft harte Blätter sowie, insbesondere bei Flybarless-Helis, eine sehr harte Dämpfung verwendet. Die Rotorblätter verbiegen sich zwar aufgrund der Kräfte, aber der „Konuswinkel“ wird deutlich kleiner sein als er sich im obigen Bild bzw. aus Gl. (4.2) ergeben würde. Bei den modernen Modellhelis spielt daher der Konuswinkel und damit der Abgleich der Blattschwerpunkte evtl. eine untergeordnete Rolle.

5. Pendel und Blattwaagen

Blattwaagen sind nichts anderes als Pendel; daher lohnt es sich kurz ein paar Punkte dazu aufzufrischen. Im folgenden Bild ist links ein Pendel so wie es in allen Lehrbüchern diskutiert wird dargestellt: Es ist eine Masse dessen Schwerpunkt sich im Abstand vom Drehpunkt befindet. Es ist klar was passiert, läßt man das Pendel los so fällt es nach unten und wird hin-und-her schwingen bis die Energie durch Reibung (vorallem im Drehlager) aufgebraucht ist und das Pendel zum Stillstand kommt. Der Schwerpunkt hängt dann exakt unterhalb des Drehpunkts. Die Schwingperiode hängt (für kleine Auslenkungen) vom Abstand ab: (siehe z.B. [6]).

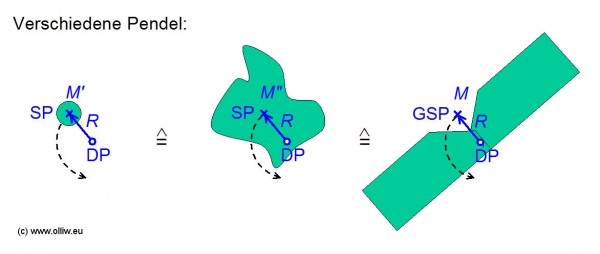
Die Masse braucht aber keine kleine Kugel sein, sondern kann irgend ein starrer Körper sein, wie z.B. der im Bild in der Mitte gezeigte Körper. Der Körper wird wieder nach unten fallen und solange schwingen bis er durch die Reibung zum Stillstand kommt, und der Schwerpunkt wieder exakt unterhalb des Drehpunkts liegt. Der Unterschied zum obigen Pendel besteht nur darin, dass die Schwingperiode nicht nur von der Pendellänge abhängt, sondern auch vom Trägheitsmoment des Körpers (siehe z.B. [7]):

      Gl. (5.1)

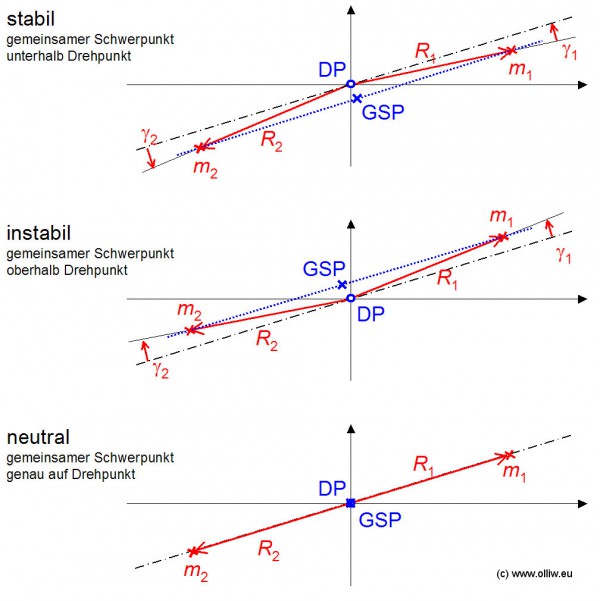
Der starre Körper kann natürlich auch aus zwei Rotorblättern bestehen, die mit einer Auswuchthilfe zusammen geschraubt wurden, wie im Bild rechts gezeigt, oder auf eine Blattwaage montiert wurden. Für die Pendelbewegung entscheidend ist hierbei wo der gemeinsame Schwerpunkt liegt. Dessen Lage hängt nun nicht nur von den Blatteigenschaften ab sondern auch davon wie die Rotorblätter montiert wurden (mehr dazu im nächsten Kapitel). Der gemeinsame Schwerpunkt ergibt sich aus der Lage der Schwerpunkte der beiden Rotorblätter entsprechend , wie im nächsten Bild angedeutet (bei Blattwaagen geht natürlich noch die Wippe mit ein).

Grundsätzlich können nun drei Situationen unterschieden werden. Befindet sich der gemeinsame Schwerpunkt oberhalb des Drehpunkts, dann wird sich der Rotor nicht stabil einpendeln, sondern wird „umklappen“, so dass der gemeinsame Schwerpunkt unterhalb des Drehpunkts zu liegen kommt. Befindet sich der gemeinsame Schwerpunkt unterhalb des Drehpunkts, pendelt sich der Rotor in eine stabile Lage ein. Ein Sonderfall besteht wenn der gemeinsame Schwerpunkt mit dem Drehpunkt genau deckungsgleich ist. Dann wird der Rotor in jeder beliebigen Lage in Ruhe verharren, und nie pendeln! Wir merken uns also:

Gemeinsamer Schwerpunkt = Drehpunkt gilt genau dann wenn sich das Pendel neutral verhält.

Jetzt sollte etwas klingeln, gemeinsamer Schwerpunkt = Drehpunkt, war das nicht genau das was wir durch’s Wuchten erreichen wollen weil sich dann die Fliehkräfte aufheben?

6. Ausbalancieren

Nachdem wir uns in Kapitel 5 ans Pendel erinnert haben, könne wir das Ausbalancieren nun genau ansehen. Zuerst wird das Auswiegen mit einer Auswuchthilfe betrachtet, die Situation bei einer Blattwaage wird am Ende des Kapitels kurz beleuchtet.

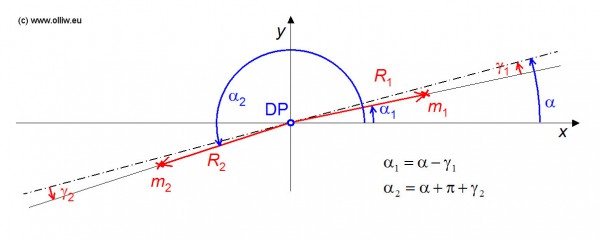
Das Ziel des Auswiegens scheint klar: Der Rotor soll so mit Tesa beklebt werden, dass er horinzontal stehen bleibt. Was heisst aber horinzontal? Nun, diese Frage wollen wir für einen Moment übergehen, und annehmen das es eine „Kante“ gibt an der wir uns orientieren können; diese Kante ist im folgenden Bild strich-gepunktelt dargestellt. Die Lage der beiden Schwerpunkte ist dann durch die Abstände , und Vorlaufwinkel , bestimmt.

Im gezeichneten Fall liegt der gemeinsame Schwerpunkt unterhalb des Drehpunkts, und der Rotor wird sich ausbalancieren. Welche Bedingung ist zu erfüllen, damit sich der Rotor horizontal ausbalanciert?

Hierzu betrachten wir zunächst das Drehmomentgleichgewicht für einen beliebigen Winkel :

  ,     Gl. (6.1)

Dies läßt sich mit den Informationen aus dem Bild umschreiben zu oder . Eine horizontale Ausrichtung des Rotors entspricht . Damit erhalten wir die

Balance-Bedingung:   .     Gl. (6.2)

Aha, fällt Euch der Unterschied zur Fliehkraft-Bedingung Gl. (2.2) [oder Gl. (3.3)] auf? Nur wenn die Vorspuren der beiden Blätter identisch sind, kann durch Auswiegen die Fliehkraft-Bedingung erfüllt werden! Ist ja eigentlich auch logisch, und hätte man sich auch ohne die ganze Rechnerei denken können: Die Gl. (6.2) läßt sich nämlich auch als schreiben, ganz entsprechend der „Kraft mal Hebellänge“ Merkregel. So einfach das Ergebnis ist, so wichtig ist es!

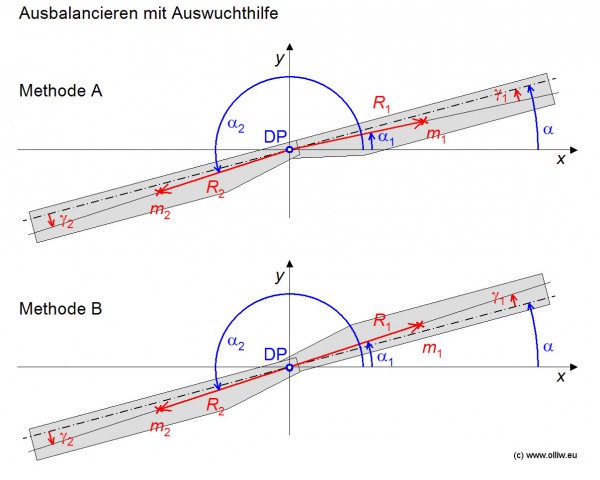
Damit können wir nun auch die Frage beantworten, ob die Rotorblätter am Besten entsprechend der Methode A oder Methode B im nachfolgenden Bild montiert werden soll. Kurze Antwort: Methode B.

Lange Antwort: In beiden Anordnungen ist die Masse des gesamten Rotors identisch, und die Trägheitsmomente sind nahezu gleich. Allerdings ist in Anordnung A der gemeinsame Schwerpunkt viel weiter vom Drehpunkt entfent als in Anordnung B, d.h., der Abstand ist viel größer. Dementsprechend ist die Periodendauer kürzer, siehe Gl. (5.1), und der Rotor pendelt sich viel schneller ein. Allerdings ist die Waage aber auch dementsprechend unempfindlicher, d.h., Unterschiede zwischen und können weniger genau ausgemessen werden [wem die eigene Erfahrung nicht reicht, das läßt sich z.B. mit Gl. (6.1) zeigen]. Neben der Genauigkeit gibt es noch einen weiteren Grund. In der Anordnung A haben wir keine Möglichkeit unterschiedliche Vorspuren zu detektieren, aber auch die Vorspuren müssen ja übereinstimmen um die Fliehkraft-Bedingung erfüllen zu können. In Anordnung B können wir die Blätter optisch so ausrichten, dass sie der geometrischen Form nach entgegengesetzt stehen (und damit die areoelastischen Kräfte ausgeglichen sind, das war zumindest eine der Grundannahmen oben!). Erreichen wir nun ein neutrales Verhalten des Rotors dann ist sichergestellt, dass nicht nur die Balance-Bedingung erfüllt ist sondern auch die Vorspuren übereinstimmen, also tatsächlich die einfache Fliehkraft-Bedingung Gl. (2.2) erfüllt ist! Ein Abgleich der Massen- oder Blattschwerpunkte ist mit beiden Methoden natürlich nicht möglich.

Die Methode B entspricht übrigens genau der Vorgehensweise beim Wuchten von Propellern (siehe z.B. [8]), oder der Vorgehensweise beim Auswuchten des gesamten Rotorkopfs (siehe wieder dieses Video [5]). Kein Wunder, die Schulphysik gilt halt auch da. 🙂

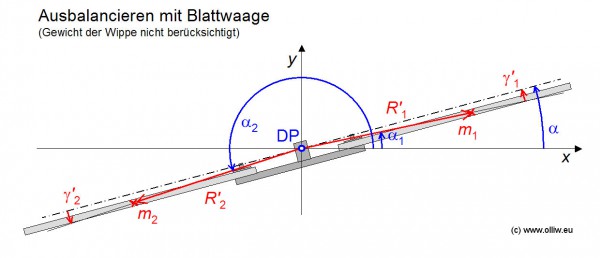
Noch ein kurzes Wort zu den Blattwaagen, siehe auch das nächste Bild. Die obigen „theoretischen“ Überlegungen gelten genauso, wenn die Winkel und nicht als Vorspuren interpretiert werden, sondern als Größen die die Bauart der Wippe beschreiben. Es gilt wieder Gl. (6.2). Abhängig von der Bauart liegt der gesamte Schwerpunkt mal mehr oder weniger unterhalb des Drehpunktes, und es gibt sogar Blattwaagen, bei denen sich der gesamte Schwerpunkt durch verschiebbare Gewichte nahe an den Drehpunkt bringen lässt. Damit trifft zumindest das Empfindlichkeits-Problem von Methode A nicht zu. Unterschiedliche Vorspuren, und damit die tatsächliche Erfüllung der einfachen Fliehkraft-Bedingung, lassen sich aber auch mit den Blattwaagen nicht bestimmen oder angleichen, und bleibt also ein Nachteil der Selbigen.

7. Zusammenfassung und Schlussfolgerungen

In den obigen Kapiteln ergaben sich einige, wenn man es recht bedenkt eigentlich sehr offensichtliche Einsichten. Wir sind bei den Überlegungen davon ausgegangen, dass die beiden Rotorblätter bzgl. ihrer aeroelastischen Eigenschaften exakt identisch sind, also das z.B. die Form der Blätter und damit die aerodynamischen Kräfte gleich sind. Etwas anderes bleibt uns auch gar nicht übrig, zumindest bei den üblichen Methoden zum Wuchten der Rotorblätter wie sie in unserem Hobby benutzt werden. Der Ausgleich der Fliehkräfte, und damit Beseitung von Unwucht, führt auf die Fliehkraft-Bedingung , Gl. (2.2). Bezüglich des Ausgleichs des Blattschwerpunkts wurden zwei Gründe aufgeführt (eine tiefere Betrachtung liefert sicher noch 1000 weitere). Einmal wird ein Einfluss der Blatthalter vermieden, wobei das natürlich kein wirklich „guter“ Grund ist, denn dieser Effekt könnte leicht durch eine entsprechende Konstruktion der Waage berücksichtigt werden. Viel wichtiger erscheint da der zweite Grund, die Ausbildung eines Konus aufgrund der Schubkräfte. Damit auch dann der Spurlauf passt ist neben der Fliehkraft-Bedingung zusätzlich noch die Konuswinkel-Bedingung , Gl. (4.3), zu erfüllen, was auf einen Ausgleich der Massen () oder Blattschwerpunkte () führt. Der Vorlauf der Blätter taucht in diesen Überlegungen nicht explizit auf. Bei Pitch Null wird er auch keine große Rolle spielen (der Luftwiderstand wird dann für beide Blätter auch bei nicht perfekt identischen Vorlaufwinkeln ähnlich sein und die Fliehkraft-Bedingung wenig verfälschen). Bei positiven oder negativen Pitch, bzw. wenn die Blätter einen Konus bilden, wurde aber implizit gefordert, dass der Vorlauf der Blätter identisch ist (gleiche aerodynamische Eigenschaften!). Zu guter Letzt wurde der Vorgang des Ausbalancieren betrachtet. Für eine waagrechte Balance ergab sich die Balance-Bedingung , Gl. (6.2). Die Fliehkraft-Bedingung läßt sich durch auswiegen also nur erfüllen, wenn sichergestellt ist, dass die Vorlaufwinkel exakt identisch sind. Dies kann eigentlich nur mit Methode B gelingen. Damit können wir drei erste Schlussfolgerungen ziehen:

– Das Auswiegen der Blätter sollte mit der Blattanordnung B erfolgen.
– Ziel ist es, ein neutrales Verhalten zu erreichen.
– Ein Angleichen der Blattschwerpunkte und/oder Blattmassen sollte durchgeführt werden.

An diesem Punkt stellt sich sofort die Frage, wie genau müssen die Bedingungen eigentlich erfüllt sein und/oder wie, mit welcher Methode, lassen sie sich am genauesten erfüllen?

Die erste Frage ist nicht leicht zu beantworten, zumindest kenne ich keine konkreten Angaben dazu welche Kräfte/Unwuchten bei einem RC-Heli erlaubt wären. Daher diese Antwort: So genau wie mit realistischem Aufwand möglich. Da mit der Größe der Blätter sowohl die Masse als auch der Schwerpunktsabstand wächst, gilt zudem grundsätzlich: Je größer die Blätter desto genauer das Auswuchten! Das Manuskript [4] gibt weitere Hinweise. Für die Bewertung einer Unwucht ist die Schwerpunktsgeschwindigkeit relevant, und zulässige Werte für einige Fälle werden angegeben. Wir können diese Näherungsformel

  ,     Gl. (7.1)

ableiten, wobei die Unwuchtmasse und dessen Abstand bezeichnet. Für ein typisches 450er-Blatt ( = 20 g) bedeutet eine Unwuchtmasse von 0.01 g am Blattschwerpunkt ( = 15 cm) bei einer Drehzahl von 3000 U/min daher eine Schwerpunktsgeschwindigkeit von ca. 10 mm/s. Damit befindet man sich in der Gütegruppe Q 16, und ist etwas besser als was für Autoreifen gefordert wird. Von den Anforderungen für z.B. Elektromotoren oder gar einer Feinwuchtung ist man weit entfernt. Bleiben wir also dabei: So genau wie mit realistischem Aufwand möglich.

Die zweite Frage, welche Auswuchtmethode am geeignetsten ist, läßt sich dagegen gut beantworten. Betrachten wir zunächst das Ausbalancieren. Die Genauigkeit hängt hier einmal von der Reibung im Drehpunkt ab. Das spricht für Magnetlager. Für kleine Blätter ist das die ideale Wahl, aber vielleicht nicht nötig (kleine Blätter = Auswuchten weniger kritisch). Für größere Blätter werden Magnetlager schnell unrealistisch. Oft werden Kugellager benutzt, aber die sind sicher nicht ideal. Zumindest sollte die Welle dann nicht direkt am Kugellager aufliegen (wie bei vielen der „billigen“ Waagen) sondern über große Metallscheiben mit den Kugellagern in Verbindung stehen (wie bei dem in [5] benutzten DuBro 499 TruSpin Balancer). Am genauesten erscheint mir tatsächlich die einfachste aller Methoden, nämlich die Welle auf zwei Flächen aufzulegen, da hier nur der Rollwiderstand wirkt. Ösen (wie hier) oder gerundete Flächen (wie hier) sind weniger ideal, da zur Reibung noch potentielle Energie dazukommt, genausowenig wie gekrümmte Flächen (Becher, Gläser, Eierbecher, usw.). Gemeint sind also ebene, gerade Flächen. Klaro, die Flächen dürfen keine Dellen, Kratzer, Schriefen, Grate, usw. haben, und sollten möglichst waagrecht ausgerichtet sein. Dünne Flächen und Metall-auf-Metall sind auch vorteilhaft. Auf dem Netz gibt es wirklich viele einfache, billige, gute, kreative Lösungen. Solche Waagen erreichen auch eine erstaunliche Präzision. Also, man merkt’s, das ist IMHO die Lösung, und bei mir sieht das so aus wie im nachfolgenden Bild. Die Genauigkeit hängt weiterhin davon ab, wie genau die horizontale Lage des Rotors bestimmt werden kann. Auch dazu gibt es auf dem Netz gute Ideen. Aber halt! Wichtig ist das nur wenn der Drehpunkt nicht mit dem Schwerpunkt übereinstimmt (stabiles Verhalten), aber wir wollen ja ein neutrales Verhalten des Rotors erreichen! Dann ist eine genau Bestimmung der horizontalen Lage irrelevant, und das ist ein weiterer guter Grund für Methode B. Wir können eine weitere Schlussfolgerung ziehen:

– Zum Auswiegen eignet sich eine einfache Anordnung zum Auflegen der Auswuchthilfe ausgezeichnet.

Damit sind wir beim Angleichen der Blattschwerpunkte und/oder Masse. Zum Auffinden und Angleichen der Blattschwerpunkte gibt es auch viele verschiedene Vorschläge, von einfach (Rasierklinge, Lineal, über Welle rollen, Laser, usw.) bis kompliziert (Einzelblatt-Waagen, Taxis Waage). Vermutlich kann mit diesen Methoden der Blattschwerpunkt genau bestimmt werden. Aber es kommt ja nicht auf die genaue Bestimmung für ein einzelnes Blatt an, sondern darauf, dass die Schwerpunkte der zwei Blätter genau übereinstimmen! Wie gut wird das wohl gehen? Stellen wir die Frage anders. Da, wenn die Fliehkraft-Bedingung erfüllt is, es im Prinzip egal ist ob die Blattschwerpunkte oder die Massen ausgeglichen werden, können wir uns zunächst ansehen wie gut das für die Massen geht. Ein 450er-Blatt wiegt etwa 20 g, und die Auflösung einer (billigen) Waage ist ca. 0.01 g (es kommt hier auf die Auflösung, nicht die Genauigkeit an!). Mit der im obigen Bild gezeigten Auswuchtwaage kann bei einem 450er-Rotor ein Masseunterschied von kleiner als 0.01 g leicht festgestellt werden, und die Fliehkraft-Bedingung damit besser als auf 0.01 g/20 g = 0.05% erfüllt werden. Insgesamt wird so also eine Übereinstimmung der Schwerpunkte der beiden Blätter auf, sagen wir, 0.067 % erreicht. Das entspricht einer Übereinstimmung von 100 um, oder 1/10 mm, oder zwei Haarbreiten! Glaubt jemand das mit den Methoden zum Angleichen der Blattschwerpunkte eine Übereinstimmung auf 100 um genau erreicht wird? Ich nicht (mit einer Taxis Waage vielleicht schon, aber wer hat eine Taxis Waage?). Wir ziehen eine letzte, etwas überraschende, Schlussfolgerung:

– Der „Ausgleich des Blattschwerpunkts“ erfolgt am besten durch Angleichen der Massen.

Aufgrund aller dieser Überlegungen komme ich zu folgender Auswuchtprozedur:

Meine Prozedur zum Wuchten der Rotorblätter
1) Vorlauf-Kontrolle: Hierzu werden beide Blätter an der Wurzel auf einen Stab gesteckt, welcher horizontal befestigt ist (mit Wasserwaage horizontale Lage überprüfen). Die Blätter sollten nun von vorne betrachtet deckungsgleich sein. Dieser Schritt dient nur als eine Art Vorkontrolle, denn ergeben sich hier (zu) große Abweichungen wird ein gutes Wuchten der Blätter schwierig oder gar nicht erst gelingen.
2) Wiegen der Blätter: Jedes Blatt wird gewogen. Ich finde es nützlich das leichtere Blatt zu markieren. Bei diesem Schritt geht es nur darum, eine Idee davon zu bekommen wie es um die Masse der Blätter steht.
3) Ausbalancieren mit Blättern in Anordnung A: Die beiden Blätter werden entsprechend der Methode A auf die Auswuchthilfe geschraubt, und ausbalanciert. Dieser Schritt dient nur dazu, eine erste grobe Angleichung zu erreichen. Idealerweise gelingt es durch aufbringen von genau so viel Tesa wie zum Massenausgleich nötig auf das leichtere Blatt eine Balance herzustellen (verschiedene Positionen am Blatt probieren). Das gelingt aber nicht immer (hängt von der „Güte“ des Blattpaars ab).
4) Massenausgleich: Jedes Blatt wird einzeln gewogen. Das leichtere Blatt wird in der Nähe der Blattwurzel so beschwert, dass die Massen übereinstimmen.
5) Ausbalancieren mit Blättern in Anordnung B: Die beiden Blätter werden nun entsprechend der Methode B auf die Auswuchthilfe geschraubt, und ausbalanciert (mit Tesa). Ziel ist ein neutrales Verhalten des Rotors. Den Rotor dazu in verschiedene Lagen bringen, er soll sich nicht bewegen. Zur Kontrolle den Rotor jeweils in die vier möglichen Richtungen bringen.
6) Feintunen: Schritte (4) und (5) solange wiederholen bis das Ergebnis zufriedenstellend ist.

Noch eine Bemerkung dazu wo die Ausgleichsmassen, bzw. der Tesafilm, angebracht werden sollten. Im Prinzip ist es völlig egal wo, solange am Ende die Blätter gewuchtet sind (der Blattschwerpunkt ist diesbezüglich in keiner Weise ausgezeichnet, im Gegensatz zu manchen Behauptungen). Beim Massenausgleich in Schritt (4) wird die Zusatzmasse sinnigerweise bei der Blattwurzel angebracht, um die Balance möglichst wenig zu verändern. Beim Ausbalancieren in Schritt (5) wird man demgegenüber die Zusatzmasse tendenziell eher am Blattende anbringen (längerer Hebel = kleinere Zusatzmasse). Es ist jedoch zu berücksichtigen, dass gerade der äußere Teil des Rotors aerodynamisch besonders wichtig ist. Das Aufbringen von (zu viel) Zusatzmasse in diesem Bereich kann die aerodynamischen Eigenschaften daher (manchmal zu stark) beeinflussen. Hier ist ein Kompromiss gefragt. Ist z.B. in Schritt (5) viel Zusatzmasse nötig, dann kann es eventuell günstiger sein diese in der Näher der Blattmitte anzubringen, auch wenn dann insgesamt mehr Zusatzmasse benötigt wird.

Appendix: Referenzen
[1] Rotorblätter auswuchten – rc-heli-fan.org [link]
[2] Blade balancing & Centre of Gravity – by HollyHeli (John Wilson) [link]
[3] Unwucht – Wikipedia [link]
[4] 12. Starrer Rotor Auswuchten – TU Darmstadt [.pdf]
[5] RC Heli Rotorkopf wuchten und balancieren – by Panavia (Tobias Schug) [link]
[6] Mathematisches Pendel – Wikipedia [link]
[7] Physikalisches Pendel – Wikipedia [link]
[8] prop balancing video tutorial – by crispyspa [link]
[9] a, b
[10] Rotorblätter – by Josef Gornik

Appendix: Formelsammlung

Schwerpunkt:   ,     Gl. (A.1)

Fliehkraft:   ,     Gl. (A.2)

Drehmoment:   ,     Gl. (A.3)

Trägheitstensor:   ,     Gl. (A.4)

Steiner’sche Satz:   ,     Gl. (A.5)

Drehimpuls:   ,     Gl. (A.6)

Bewegungsgleichung:   ,     Gl. (A.7)